Как находить коэффициент: Числовой коэффициент выражения: определение, примеры

Числовой коэффициент выражения: определение, примеры

В математических описаниях часто фигурирует термин «числовой коэффициент», например, в работе с буквенными выражениями и выражениями с переменными. Материал статьи ниже раскрывает понятие этого термина, в том числе, на примере решения задач на нахождение числового коэффициента.

Определение числового коэффициента. Примеры

Учебник Н.Я. Виленкина (учебный материал для учащихся 6 классов) задает такое определение числового коэффициента выражения:

Определение 1

Если буквенное выражение является произведением одной или нескольких букв и одного числа, то это число называется числовым коэффициентом выражения.

Числовой коэффициент зачастую называют просто коэффициентом.

Данное определение дает возможность указать примеры числовых коэффициентов выражений.

Пример 1

Рассмотрим произведение числа 5 и буквы a, которое будет иметь следующий вид: 5·a. Число 5 является числовым коэффициентом выражения согласно определению выше.

Еще пример:

Пример 2

В заданном произведении x·y·1,3·x·x·z десятичная дробь 1,3 – единственным числовой множитель, который и будет служить числовым коэффициентом выражения.

Также разберем такое выражение:

Пример 3

7·x+y. Число 7 в данном случае не служит числовым коэффициентом выражения, поскольку заданное выражение не является произведением. Но при этом число 7 – числовой коэффициент первого слагаемого в заданном выражении.

Пример 4

Пусть дано произведение 2·a·6·b·9·c.

Мы видим, что запись выражения содержит три числа, и, чтобы найти числовой коэффициент исходного выражения, его следует переписать в виде выражения с единственным числовым множителем. Собственно, это и является процессом нахождения числового коэффициента.

Отметим, что произведения одинаковых букв могут быть представлены как степени с натуральным показателем, поэтому определение числового коэффициента верно и для выражений со степенями.

К примеру:

Пример 5

Выражение 3·x3·y·z2– по сути оптимизированная версия выражения 3·x·x·x·y·z·z, где коэффициент выражения – число 3.

Отдельно поговорим о числовых коэффициентах 1 и -1. Они очень редко записаны в явном виде, и в этом их особенность. Когда произведение состоит из нескольких букв (без явного числового множителя), и перед ним обозначен знак плюс или вовсе нет никакого знака, мы можем говорить, что числовым коэффициентом такого выражения является число 1. Когда перед произведением букв обозначен знак минус, можно утверждать, что в этом случае числовой коэффициент – число -1.

Далее определение числового коэффициента расширяется с произведения нескольких букв и числа до произведения числа и нескольких буквенных выражений.

Пример 6

К примеру, в произведении -5·x+1 число -5 будет служить числовым коэффициентом.

По аналогии, в выражении 8·1+1x·xчисло 8 – коэффициент выражения; а в выражении π+14·sinx+π6·cos-π3+2·x числовой коэффициент  — π+14.

Нахождение числового коэффициента выражения

Выше мы говорили о том, что если выражение представляет собой произведение с единственным числовым множителем, то этот множитель и будет являться числовым коэффициентом выражения. В случае, когда выражение записано в ином виде, предстоит совершить ряд тождественных преобразований, который приведет заданное выражение к виду произведения с единственным числовым множителем.

Пример 7

Задано выражение −3·x·(−6). Необходимо определить его числовой коэффициент.

Решение

Осуществим тождественное преобразование, а именно произведем группировку множителей, являющихся числами, и перемножим их. Тогда получим: −3·x·(−6)=((−3)·(−6))·x=18·x.

В полученном выражении мы видим явный числовой коэффициент, равный 18.

Ответ: 18

Пример 8

Задано выражение a-12·2·a-6-2·a2-3·a-3. Необходимо определить его числовой коэффициент.

Решение

С целью определения числового коэффициента преобразуем в многочлен заданное целое выражение. Раскроем скобки и приведем подобные слагаемые, получим:

a-12·2·a-6-2·a2-3·a-3==2·a2-6·a-a+3-2·a2+6·a-3=-a

Числовым коэффициентом полученного выражения будет являться число -1.

Ответ: -1.

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Автор:
Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Химические уравнения — как расставлять коэффициенты?

Химическое уравнение — это условная запись химического превращения с помощью химических формул и математических знаков

При составлении химических уравнений используют математические знаки «+», «−», «=», а также числа — они выступают в качестве коэффициентов и индексов.

Коэффициенты показывают число частиц (атомов или молекул), а индексы — число атомов, которые входят в состав молекулы.

Химическую реакцию можно изобразить в виде схемы:

На схеме протекание реакции представлено нагляднее, но сложные химические процессы изобразить таким способом сложно. Поэтому их записывают в виде химического уравнения.

Вещества, которые вступают в реакцию, называют исходными веществами, или реагентами. Вещества, которые образуются в результате, называют продуктами реакции.

Давайте разберем этот пример химического уравнения. Здесь видно, что из двух молекул водорода и одной молекулы кислорода образуются две молекулы воды. Реагенты в данном случае — водород и кислород, продукт реакции — вода.

Новые вещества образуются вследствие перегруппировки исходных атомов. В результате химической реакции атомы химических элементов никуда не исчезают и не возникают новые, их число остается неизменным — это следует из закона сохранения массы веществ.

Закон сохранения массы веществ

Масса веществ, вступивших в реакцию, равна массе веществ, образовавшихся в ходе этой реакции.

Закон сохранения массы веществ лежит в основе химии и используется при составлении уравнений химических реакций.

Алгоритм составления уравнения химической реакции

Рассмотрим, как составлять уравнения химических реакций, на примере взаимодействия магния и кислорода с образованием оксида магния.

1. Записываем химические формулы исходных веществ в левой части уравнения. Напоминаем: молекулы H₂, N₂, O₂, F₂, Cl₂, Br₂, I₂ двухатомны. Между исходными веществами ставим «+», а затем знак «=».

2. После знака равенства записываем химическую формулу продукта. Химическую формулу необходимо составить с учетом валентностей химических элементов.

3. Согласно закону сохранения массы веществ, число атомов каждого химического элемента до и после реакции должно быть одинаковым. Давайте посмотрим, как расставлять коэффициенты в химических уравнениях, чтобы закон выполнялся.

   Из составленной химической реакции видно, что количество атомов магния слева и справа от знака равенства одинаково, но атомов кислорода слева два, а справа один.

   Чтобы уравнять число атомов в химическом уравнении, находим наименьшее общее кратное (НОК), в нашем случае — 2. А затем делим НОК на количество атомов кислорода в реагентах и полученное число записываем в виде коэффициента.

   Это важно

   Коэффициент 1 в уравнении химической реакции не указывается, но при подсчете суммы коэффициентов в уравнении его необходимо учитывать.

4. Проверим количество атомов магния до и после знака «=». Если перед химической формулой уже стоит коэффициент, то для подсчета количества атомов необходимо умножить коэффициент на индекс, который относится к этому химическому элементу.

5. Чтобы уравнять количество атомов магния в химической реакции, посчитаем НОК и разделим его на количество атомов с каждой стороны от знака «=». Результат деления и будет являться коэффициентом (повторяем расстановку коэффициентов в химическом уравнении из 3-го пункта).

6. Получаем уравнение химической реакции, в котором в исходных веществах и продуктах реакции по 2 атома магния и кислорода.

Сумма коэффициентов в этом химическом уравнении равна 5 (2 + 1 + 2 = 5).

Коэффициенты, которые стоят в химическом уравнении перед веществами, указывают на мольное соотношение исходных веществ и продуктов реакции, по которому и производятся расчеты.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Типы химических реакций

Химические реакции можно классифицировать по различным признакам:

1. По числу и составу исходных веществ и продуктов реакции.

2. По изменению степени окисления.

3. По тепловому эффекту.

4. По агрегатному состоянию.

5. По наличию или отсутствию катализатора.

6. По обратимости.

По числу и составу исходных веществ и продуктов реакции

По этому признаку выделяют 4 типа реакций: реакции соединения, реакции разложения, реакции замещения и реакции обмена.

Реакции соединения — это реакции, в результате которых из нескольких более простых веществ образуется одно более сложное.

Например, простые вещества барий и кислород взаимодействуют с образованием сложного вещества оксида бария:

2Ba + O₂ = 2BaO.

Также к реакциям соединения относится взаимодействие оксида натрия с водой с образованием более сложного вещества гидроксида натрия. Оно более сложное, так как состоит уже из трех атомов химических элементов, в отличие от веществ-реагентов, которые состоят из двух атомов:

Na₂O + H₂O = 2NaOH.

Реакции разложения — это реакции, в результате которых из одного более сложного вещества образуется несколько более простых веществ. Является процессом, обратным реакции соединения.

Пример такой реакции — разложение нитрата серебра на несколько более простых веществ: серебро, оксид азота (IV) и кислород.

2AgNO₃ = 2Ag + 2NO₂↑ + O₂↑.

Что это за стрелочка? 🤔

Стрелка вверх означает, что получившееся вещество является газом, который покидает место проведения реакции и больше не участвует в ней.

Реакции замещения — это такие реакции, в результате которых атомы простого вещества замещают атомы одного химического элемента в сложном веществе. Также возможно замещение функциональных групп в сложном веществе.

Например, замещение атомов водорода в молекуле соляной кислоты на атомы цинка:

Zn + 2HCl = ZnCl₂ + H₂↑.

Реакции обмена — это реакции между двумя сложными веществами, в результате которых вещества обмениваются своими составными частями.

Например, NaOH + H₂SO₄ = Na₂SO₄ + H₂O.

Реакции нейтрализации

Реакция щелочи с кислотой называется реакцией нейтрализации и является частным случаем реакции обмена.

Для наглядности показали все типы химических реакций по этому признаку на схеме:

По изменению степени окисления

По этому признаку выделяют два вида реакций:

• реакции, протекающие без изменения степени окисления;

• окислительно-восстановительные реакции (ОВР) — реакции, протекающие с изменением степени окисления нескольких элементов.

В ОВР всегда участвуют вещество-окислитель и вещество-восстановитель. Другие исходные вещества, принимающие участие в реакции, выступают в качестве среды, в которой протекает эта реакция.

Окислитель — вещество, в состав которого входит ион или атом, который в процессе реакции принимает электроны, тем самым понижая свою степень окисления.

Восстановитель — вещество, в состав которого входит ион или атом, который в процессе реакции отдает электроны, тем самым повышая свою степень окисления.

Из определений можно сделать вывод, что в ходе реакции протекает два процесса: принятие электронов (восстановление) и отдача электронов (окисление). Протекают они одновременно.

По тепловому эффекту

По тепловому эффекту реакции делятся на эндотермические и экзотермические.

Эндотермические реакции протекают с поглощением теплоты (−Q). Буквой Q обозначается количество теплоты.

К таким реакциям относятся практически все реакции разложения. Пример:

CaCO₃ = CaO + CO₂ − Q.

Экзотермические реакции протекают с выделением теплоты (+Q).

К таким реакциям относятся практически все реакции соединения. Пример:

2H₂ + O₂ = 2H₂O + Q.

По агрегатному состоянию исходных веществ

По этому признаку все реакции разделяют на гомогенные и гетерогенные.

Гомогенные реакции протекают в одной фазе.

К гомогенным реакциям относятся те, исходные вещества которых находятся либо в жидком агрегатном состоянии, либо в газообразном. Например, взаимодействие двух газообразных веществ — водорода и хлора:

H₂(г) + Cl₂(г) = 2HCl.

Агрегатное состояние указывается в правом нижнем углу: «г» — газообразное, «ж» — жидкое, «тв» — твердое.

Гетерогенные реакции протекают на границе раздела фаз.

Как правило, такие реакции протекают между веществами, которые находятся в разных агрегатных состояниях:

2Na(тв) + 2H₂O(ж) = 2NaOH + H₂.

Также к гетерогенным относятся реакции между двумя несмешивающимися жидкостями. Собрали несколько примеров гетерогенных реакций:

Коэффициент — Определение, Примеры | Коэффициент переменной

В математике коэффициент — это число или любой символ, представляющий постоянное значение, умноженное на переменную одного члена или членов многочлена. Обычно это число, но иногда его можно заменить буквой в выражении. Например, в выражении: ax ² + bx + c, x — переменная, а «a» и «b» — коэффициенты.

1.	Что такое коэффициент?
2.	Коэффициент переменной
3.	Как найти коэффициент?
4.	Числовой коэффициент
5.	Старший коэффициент
6.	Часто задаваемые вопросы о коэффициенте

Что такое коэффициент?

Коэффициент относится к числу или количеству, помещенному в переменную. Обычно это целое число, которое умножается на переменную и записывается рядом с ней. Предполагается, что переменные, не имеющие номера, имеют коэффициент 1. Например, в выражении 3x 3 — это коэффициент при x, а в выражении x ² + 3 1 — это коэффициент при x ² . Другими словами, коэффициент — это мультипликативный коэффициент в терминах полинома, ряда или любого выражения. Обратите внимание на следующее выражение, которое показывает, что 5 — это коэффициент при x ² , а 8 — это коэффициент при y.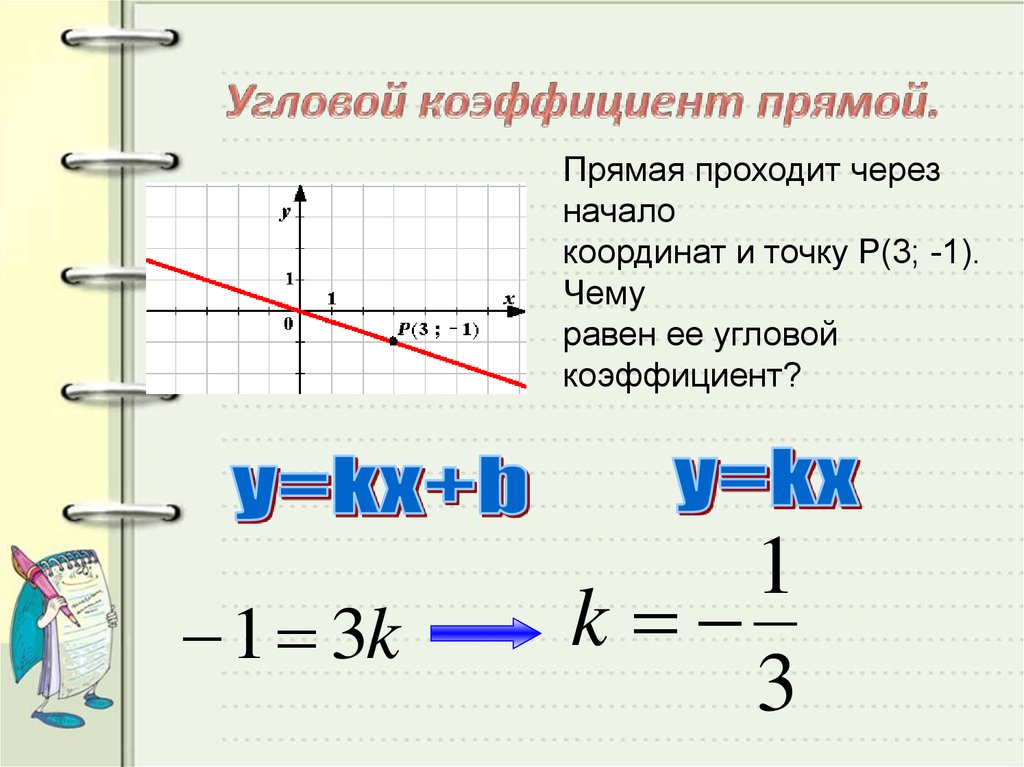

Коэффициент может быть положительным или отрицательным, действительным или мнимым, в виде десятичных знаков или дробей. Другое определение коэффициента в гласит: «Любое число, на которое мы умножаем переменную».

Коэффициент переменной

Коэффициент переменной — это значение целого числа или любой буквы, которая присутствует в переменной. Например, коэффициент при переменной x в выражении 2x + 3y равен 2, а в том же выражении коэффициент при переменной y равен 3. Аналогично, коэффициент при переменной x ² в квадратном выражении ax ² +bx+c есть а.

Как найти коэффициент?

Чтобы найти коэффициент переменной в термине, выполните шаги, указанные ниже:

• Шаг 1: Обведите переменную вместе с ее степенью, коэффициент которой мы находим.
• Шаг 2: Оставьте эту переменную и рассмотрите все другие числа или переменные, записанные с ней. Это будет коэффициент.

Например, найдем коэффициенты при x и y в члене 5xy. Чтобы найти коэффициент x, мы можем обвести его или подчеркнуть. Затем возьмите все остальное, кроме x, т.е. 5y. Итак, коэффициент при x в члене 5xy равен 5y. Точно так же коэффициент y в термине 5xy равен 5x.

Чтобы найти коэффициент , самое главное, что следует помнить, это то, что он всегда идет с переменной. Разберем это на примере: 5x ² +2y-7. В этом выражении мы видим три члена: 5x ² , 2y и -7. В первом члене 5x ² , x ² — переменная, а поскольку мы знаем, что коэффициент всегда идет с переменной, поэтому коэффициент равен 5. Во втором члене 2y, y — переменная, поэтому коэффициент равен 2. В третьем члене -7 известно как константа, а не коэффициент.

Числовой коэффициент

Числовой коэффициент — это число, представляющее собой множитель переменных в термине. Например, 3 — числовой коэффициент члена 3мн. Термин числовой коэффициент используется для постоянных множителей переменной. Типичный пример — 4xy. Здесь числовой коэффициент xy равен 4.

Старший коэффициент

Когда полином записывается в стандартной форме, то коэффициент члена, содержащего степень, или коэффициент, записанный с первым членом, называется старшим коэффициентом. Другими словами, это коэффициент члена с наибольшей степенью в выражении. Посмотрите на изображение ниже, показывающее старший коэффициент в общей форме многочлена.

Некоторые примеры старшего коэффициента в многочленах приведены ниже:

• В выражении 4a ² — 7a + 9 старший коэффициент равен 4.
• В 3xy — 9x + 4 старший коэффициент равен 3.
• В 17 — 3х ³ + 5ху + 8х, старший коэффициент -3.

Советы и рекомендации по коэффициентам

При работе с коэффициентами помните о следующих моментах:

• К переменной всегда присоединяется коэффициент.
• Переменная без номера имеет коэффициент 1.
• Мы не можем иметь 0 в качестве коэффициента, так как значение члена с 0 в качестве коэффициента равно 0.

Нестандартное мышление!

• Может ли переменная быть коэффициентом?
• Может ли дробь быть коэффициентом?

☛ Похожие темы:

Ознакомьтесь с интересными статьями о коэффициенте. Нажмите на них, чтобы узнать больше!

• Как рассчитать коэффициент корреляции
• Выражение: член, множитель и коэффициент
• Соотношения между коэффициентами природы растворов

Примеры коэффициентов

1. Пример 1: В выражении ax ² +bx+c укажите коэффициент при члене x ² .

   Решение: В приведенном выше выражении мы видим, что в термине ax ² , x — переменная.

   Ответ: Следовательно, коэффициент равен «а».

2. Пример 2: Найдите числовые коэффициенты в следующем алгебраическом выражении: 3x ² -2y+5.

   Решение: В данном выражении три слагаемых. В члене 3x ² числовой коэффициент равен 3, в -2y коэффициент равен -2, а 5 является константой.

   Ответ: Таким образом, числовые коэффициенты равны 3 и -2.

3. Пример 3: Найдите коэффициенты в следующем выражении: x ³ +2x+3.

    

   Решение: В приведенном выше выражении есть три члена. В члене x ³ коэффициент равен 1. В 2x он равен 2, а 3 — константа.

   Ответ: Следовательно, коэффициенты равны 1 и 2.

перейти к слайдуперейти к слайдуперейти к слайду

Развивайте логическое мышление и укрепляйте его уверенность!

Воспитайте логических мыслителей и укрепите их уверенность! Благодаря гибкому учебному плану Куэмат выходит за рамки традиционных методов обучения. Мы делаем математику увлекательной. Проверьте, как!

Записаться на бесплатный пробный урок

Практические вопросы по коэффициенту

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о коэффициенте

Что означает коэффициент в математике?

Коэффициент — это число или алфавит, который умножается на переменную одного члена или членов многочлена. Например, в термине 7x 7 является коэффициентом. Коэффициент x в члене 3xy равен 3y.

Как найти коэффициент?

Чтобы найти коэффициент, мы можем покрыть переменную и найти присутствующие в ней числа или алфавиты. Например, чтобы найти коэффициент при m в члене 10mn, мы можем скрыть m, и тогда у нас останется 10n, который является искомым коэффициентом.

Может ли коэффициент быть отрицательным?

Да, коэффициент может быть и отрицательным. Например, в термине -9x, -9 является коэффициентом.

Может ли дробь быть коэффициентом?

Да, дробь тоже может быть коэффициентом.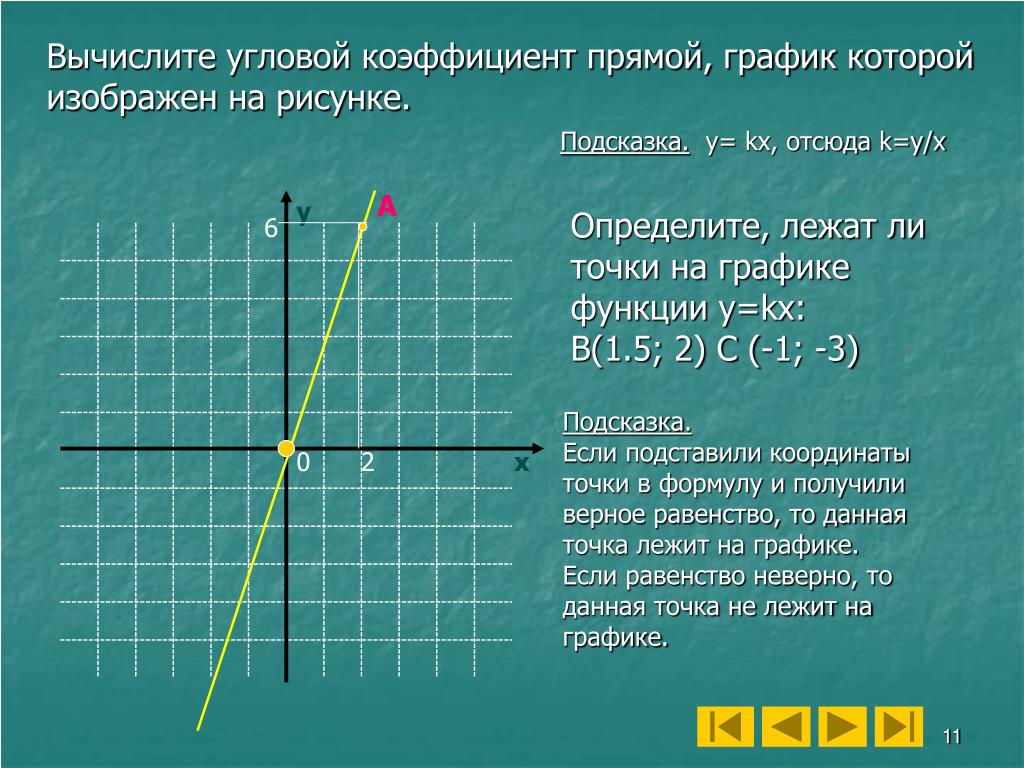 Например, в выражении: (3/4)x + 2 3/4 — дробь, являющаяся коэффициентом при x.

Что такое коэффициент 0?

Коэффициент 0 сам по себе равен 0, поскольку 0 можно записать как 0, умноженное на некоторую переменную, скажем, 0x. Тогда коэффициент x в 0x равен 0,

Может ли коэффициент равняться нулю?

Коэффициент не может быть равен нулю, поскольку при умножении 0 (в качестве коэффициента) на любую переменную значение члена дает 0. Однако коэффициент может быть любым натуральным числом, отрицательным числом, десятичной дробью или дробью.

Что такое числовой коэффициент в математике?

Термин числовой коэффициент используется для множителей переменной, которые представлены в виде действительных чисел. Типичный пример — 4xy. Здесь числовой коэффициент xy, x или y равен 4,9.0007

Что такое ведущий коэффициент?

Старший коэффициент определяется как коэффициент члена с наибольшей степенью в многочлене. Например, в выражении 4 + 3x ² 3 является старшим коэффициентом.

Какой коэффициент x²?

Коэффициент переменной без цифр или букв всегда равен 1. Таким образом, коэффициент x ² равен 1.

Что такое коэффициент константы?

Вопрос «коэффициент константы» не имеет смысла, так как нет темы коэффициента, если нет переменной.

Что такое пример коэффициента?

Коэффициент определяется как число или алфавит, присоединенные к переменной в термине. Например, коэффициент x в члене 5x ⁵ равен 5, коэффициент q в 9pq равен 9p и т. д. коэффициент

Все ресурсы по алгебре 1

10 Диагностические тесты
557 практических тестов
Вопрос дня
Карточки
Учитесь по концепции

Алгебра 1 Помощь »
Переменные »
Полиномы »
Биномы »
Как найти значение коэффициента

Укажите коэффициент в произведении

.

Возможные ответы:

Правильный ответ:

Объяснение:

Хотя эту задачу можно решить, умножив три бинома, это не обязательно. Есть три способа умножения одного члена из каждого бинома таким образом, чтобы умножались два члена и одна константа; найдите три продукта и добавьте их следующим образом: 9Добавить

Правильный ответ .

Сообщить об ошибке

Укажите коэффициент в произведении  

Возможные ответы:

Правильный ответ:

7

Объяснение:

Хотя эту задачу можно решить, умножив три бинома, это не обязательно. Есть три способа умножения одного члена из каждого бинома таким образом, чтобы умножались два члена и одна константа; найдите три продукта и добавьте их следующим образом:

Добавить:

Сообщить об ошибке

Укажите коэффициент в биномиальном разложении .

Возможные ответы:

Правильный ответ:

Объяснение:

Если выражение расширить, то по биномиальной теореме член равен

или, эквивалентно, коэффициент IS

Следовательно, коэффициент можно определить путем установки

:

Отчет о ошибке

. биномиальное расширение .

Возможные ответы:

Правильный ответ:

Объяснение:

Если выражение расширить, то по биномиальной теореме член равен

или, эквивалентно, коэффициент IS

Следовательно, коэффициент можно определить путем установки

:

Отчет о ошибке

. биномиальное расширение .

Возможные ответы:

Правильный ответ:

Объяснение:

Если выражение расширить, то по биномиальной теореме член равен

или, эквивалентно, коэффициент IS

Следовательно, коэффициент можно определить путем установки

Отчет о ошибке

. продукт

.

Возможные ответы:

Правильный ответ:

Объяснение:

Хотя эту задачу можно решить, умножив три бинома, это не обязательно. Есть три способа умножения одного члена из каждого бинома таким образом, чтобы умножались два члена и одна константа; найдите три продукта и добавьте их следующим образом:

Добавить:

Правильный ответ составляет -122.

Сообщить об ошибке

Каково значение коэффициента ?

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы определить коэффициент, нам нужно будет полностью упростить это выражение.