Можно ли сзвм сдать на бумажном носителе: Как сдать СЗВ-М на бумаге

Зарплата и управление персоналом 8 – Учет без забот

Опубликовано 16.01.2020 20:42

Автор: Administrator

Просмотров: 214888

Ох и навели шумихи эти электронные трудовые книжки! И хоть о них начали говорить ещё год назад, интерес к этой теме усилился, когда подошло время сдачи первых отчётов, отражающих кадровые изменения. В статье рассмотрим порядок работы с новыми формами в программе 1С: Зарплата и управление персоналом 8 редакции 3.

Наверно, вы неоднократно работали с сотрудниками, теряющими бумажные трудовые книжки и приносящими дубликаты? А сколько случаев ведения нескольких трудовых одновременно? И это я молчу про неверные или некорректные записи, сделанные предыдущими кадровиками. Благодаря переходу на электронные трудовые книжки, эти ситуации уходят в историю.

Ещё одним плюсом является то, что хранение трудовых больше не нужно обеспечивать работодателю. Ведь когда в организации работает 10 человек, это не составляет особого труда. А вот если 300 – становится проблематично.

Для работников тоже есть свои плюсы в переходе на электронные версии книжек. Во-первых, это защита работника от недобросовестных работодателей. Ведь теперь у работника будет возможность проверить своё трудоустройство. Во-вторых, данный вид трудовых книжек обеспечивает более надёжную сохранность данных. И в-третьих, при дистанционном трудоустройстве теперь не будет необходимости отправлять по почте свою трудовую книжку.

С 2021 года для впервые принимаемых на работу сотрудников предусмотрена выдача лишь электронных трудовых книжек. А вот у сотрудников, имеющих бумажный экземпляр есть выбор, сделав который, они обязаны до 31 декабря 2020 года уведомить своего работодателя с помощью заявления. В связи с этим, работодатели должны донести всю информацию, связанную с переходом на электронные трудовые книжки, до своих сотрудников под их личную подпись.

После получения от работника заявления, его необходимо ввести в программу и включить в соответствующие отчётные формы. Рассмотрим ввод данного заявления в 1С: ЗУП.

Для начала, необходимо проверить, какой релиз программы у вас установлен. Для этого в правом верхнем углу выберите пункт меню «О программе». 

В открывшемся окне в пункте «Конфигурация» указан номер установленного релиза программы. Для 1С: ЗУП редакция 3 он должен быть не меньше 3.1.12.113.

После проверки актуальности программного продукта переходим в раздел «Отчётность, справки» и выбираем пункт «Электронные трудовые книжки».

В открывшемся окне нажимаем на кнопку «Создать» и из выпадающего списка выбираем «Заявление о предоставлении сведений о трудовой деятельности». При помощи кнопки «Подбор» или кнопки «Добавить» нужно внести списком сотрудников, от которых были получены заявления о переходе на электронные трудовые книжки или, наоборот, о сохранении бумажного носителя. В одном заявлении можно указывать работников, выбравших разные варианты, как на рисунке ниже.

Хочется напомнить, что если сотрудник выбрал переход на электронную трудовую книжку, то в дальнейшем нельзя будет передумать и вернуться к бумажному экземпляру.

При получении заявления работодатель выдаёт бумажную трудовую книжку на руки работнику и освобождается от ответственности за её ведение и хранение. При выдаче трудовой книжки в неё вносится запись о подаче работником такого заявления.

При вводе заявлений в программу есть возможность их распечатать. Для этого необходимо нажать на кнопку .

Если сотрудник сделал выбор в пользу бумажной книжки, то в заявлении указывается статья 66 ТК РФ. А если выбор пал на электронную версию, то необходимо ссылаться на статью 66.1 ТК РФ.

Второй документ, недавно реализованный в 1С – это форма ежемесячной отчётности СЗВ-ТД, которую мы впервые будем сдавать уже 17 февраля 2020 года. Данный отчёт нужно представлять только тем предприятиям, у которых имели место кадровые перемещения и увольнения в январе 2020 года. А также те, кто получил от своих работников заявления с выбором формы трудовой книжки. Вводится данный документ при помощи кнопки «Создать» и выбором из выпадающего меню пункта «Сведения о трудовой деятельности работника, СЗВ-ТД». Для того, чтобы форма заполнялась в автоматическом порядке необходимо в кадровых документах устанавливать флаг «Отразить в трудовой книжке». Для рассмотрения заполнения формы СЗВ-ТД я создам три кадровых документа: приём на работу, кадровый перевод и увольнение.

Если забыть установить флаг об отражении операции в трудовой книжке, то форма автоматически заполнена не будет. Вернёмся к созданию отчёта СЗВ-ТД. Его можно ввести из пункта «Электронные трудовые книжки», либо с раздела «Кадры», либо с «Отчётность, справки». В открывшемся окне выберем отчётный период и нажмём на кнопку «Заполнить».

Программа заполнит табличную часть сотрудниками, по которым были кадровые передвижения. Так же по двум из них заранее были введены заявления о переходе на электронную трудовую книжку, либо о сохранении ими бумажного носителя. Эти заявления тоже попали в форму отчётности в автоматическом порядке. Если дважды кликнуть на конкретную строку, откроется окно с более подробной информацией о сотруднике и его мероприятиях.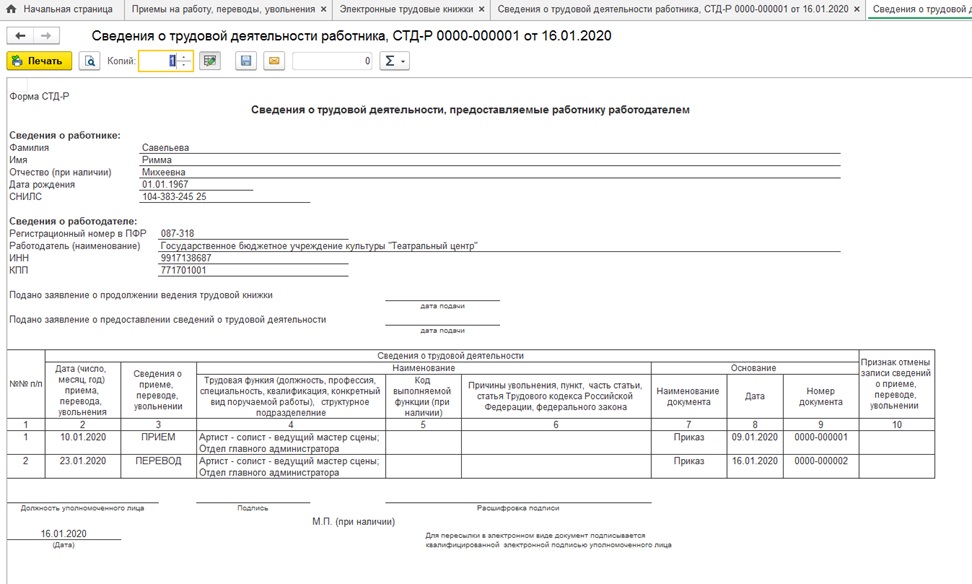

После проведения отчёта его можно распечатать по кнопке «СЗВ-ТД», выгрузить или отправить, предварительно проведя проверку. Все необходимые кнопки реализованы в верхней части формы и работаю так же, как и в других отчётах. 

И последний документ, который мы рассмотрим – это форма СТД-Р, которая вошла в перечень справок, выдаваемых сотруднику при увольнении. Так же данную форму работник имеет право запросить в случае необходимости подтверждения трудового стажа, например, при согласовании кредита в банке. То есть СТД-Р заменит нам в дальнейшем заверенную копию бумажной трудовой книжки. Сформировать её можно, как из окна «Электронные трудовые книжки» при помощи кнопки «Создать», так и на основании работника в справочнике «Сотрудники» (раздел «Кадры»).

Если СТД-Р вводить на основании сотрудника, то в открывшемся окне автоматически будут заполнены персональные данные работника, организация, в которой он трудоустроен, дата заполнения и сведения о расторжении трудового соглашения.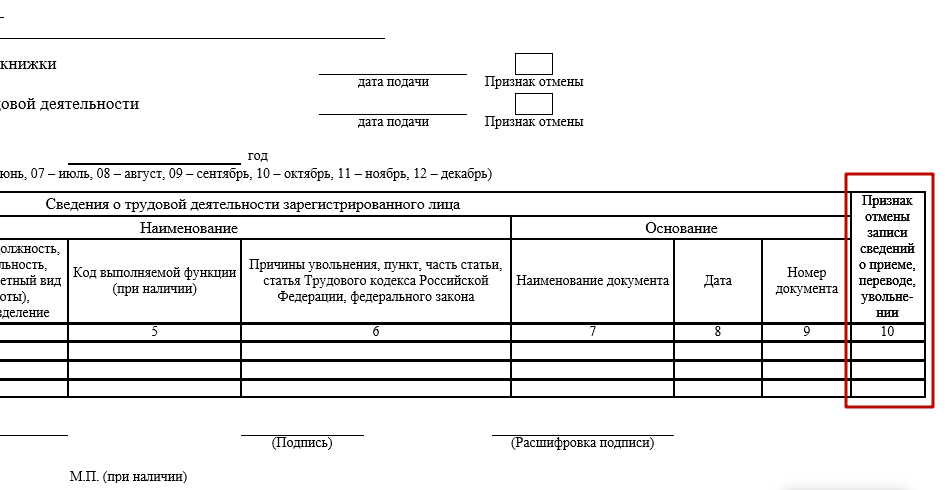

В верхней части окна есть стандартная иконка с изображением принтера, при помощи которой выводится печатная форма документа.

Автор статьи: Алина Календжан

Понравилась статья? Подпишитесь на рассылку новых материалов

Добавить комментарий

Надо ли сдавать отчет СЗВ-ТД в отношении председателя ТСЖ

Надо ли сдавать отчет СЗВ-ТД в отношении председателя ТСЖ — БУХ.1С, сайт в помощь бухгалтеру

Новости для бухгалтера, бухучет, налогообложение, отчетность, ФСБУ, прослеживаемость и маркировка, 1С:Бухгалтерия

• Новости
• Статьи
• Вопросы и ответы
• Видео
• Форум

28.04.2020

Минтруд разъяснил, надо ли сдавать в информационную систему ПФР сведения о трудовой деятельности (по форме СЗВ-ТД) в отношении председателя ТСЖ.

В письме от 16.03.2020 № 14-2/В-269 отмечается, что отношения, связанные с созданием и деятельностью товариществ собственников жилья (ТСЖ), прав и обязанностей их членов регулируются жилищным законодательством (статья 4 ЖК РФ).

По нормам ЖК РФ членство в ТСЖ возникает на основании заявления и прекращается на основании заявления или прекращения права собственности члена товарищества на помещение в многоквартирном доме.

Соответственно, деятельность членов товарищества, в том числе членов правления ТСЖ, которые избираются из числа членов ТСЖ, осуществляется не на основе трудового договора.

Учитывая, что ТСЖ образуется путем добровольного членства, между членами товарищества не могут возникать трудовые отношения, поскольку в этих отношениях отсутствуют участники трудовых отношений: наемный работник и работодатель, использующий наемный труд.

Таким образом, деятельность члена правления ТСЖ осуществляется на гражданско-правовой основе и регулируется исключительно нормами гражданского законодательства.

Учитывая, что сведения о трудовой деятельности формируются на всех зарегистрированных лиц, с которыми заключены или прекращены трудовые (служебные) отношения, сведения о трудовой деятельности в отношении председателей товарищества собственников жилья не представляются в информационную систему ПФР.

Темы:
персонифицированный учет, СЗВ-ТД, сведения о трудовой деятельности, ТСЖ

Рубрика:
Отчетность в ПФР

Подписаться на комментарии

Отправить на почту

Печать

Написать комментарий

Перспективы ставок НДФЛ, временный мораторий ПФР на штрафы и новые налоговые льготы: самые хорошие новости недели
Заполнение СЗВ-ТД, СЗВ-М и СЗВ-СТАЖ по мобилизованным сотрудникам в «1С:Зарплате и управлении персоналом 8» ред. 3
Как работодателям отчитываться в ПФР по мобилизованным сотрудникам
Работодателей не будут штрафовать за вынужденную задержку отчетов СЗВ-ТД по мобилизованным сотрудникам
Оформление МЧД для госорганов и внебюджетных фондов в программах 1С

Опросы

Кто читает БУХ. 1С

Кем вы работаете?

бухгалтер

руководитель компании

аудитор

чиновник

юрист

кадровик

специалист-внедренец

разработчик ПО

журналист

другое

Мероприятия

Все мероприятия

Метод опорных векторов (SVM) Объяснение алгоритма

Итак, вы работаете над задачей классификации текста. Вы уточняете свои тренировочные данные и, возможно, даже экспериментировали с Наивным Байесом. Вы уверены в своем наборе данных и хотите сделать еще один шаг вперед.

Введите Метод опорных векторов (SVM) , быстрый и надежный алгоритм классификации, который очень хорошо работает с ограниченным объемом данных для анализа.

Возможно, вы копнули глубже и наткнулись на такие термины, как линейно разделяемые , хитрость ядра и функции ядра . Но не бойтесь! Идея, лежащая в основе алгоритма SVM, проста, и его применение в NLP не требует большинства сложных вещей.

В этом руководстве вы узнаете об основах SVM и о том, как использовать его для классификации текста. Наконец, вы увидите, как легко начать работу с таким инструментом, не требующим написания кода, как MonkeyLearn.

Начните классифицировать текст с помощью SVM

ПОПРОБУЙТЕ СЕЙЧАС

• Что такое машины опорных векторов?
• Как работает SVM?
• Использование SVM с классификацией естественного языка
• Учебное пособие по простому классификатору SVM

Что такое машины опорных векторов?

Машина опорных векторов (SVM) — это контролируемая модель машинного обучения, которая использует алгоритмы классификации для задач классификации с двумя группами. Предоставив модели SVM наборы помеченных обучающих данных для каждой категории, они могут классифицировать новый текст.

По сравнению с более новыми алгоритмами, такими как нейронные сети, у них есть два основных преимущества: более высокая скорость и лучшая производительность при ограниченном количестве выборок (в тысячах). Это делает алгоритм очень подходящим для задач классификации текста, где обычно имеется доступ к набору данных, состоящему не более чем из пары тысяч помеченных образцов.

Как работает SVM?

Основы работы с методами опорных векторов и принцип их работы лучше всего понять на простом примере. Представим, что у нас есть два тега: красный и синий , и наши данные имеют две особенности: x и y . Нам нужен классификатор, который, учитывая пару координат (x,y) , выводит, если это либо красный , либо синий . Мы наносим наши уже размеченные данные обучения на плоскость:

Наши размеченные данные

Машина опорных векторов берет эти точки данных и выводит гиперплоскость (которая в двух измерениях представляет собой просто линию), которая лучше всего разделяет теги. Эта линия граница решения : все , что попадает в одну сторону от нее , мы будем классифицировать как синий , а все , что попадает в другую , как красный .

В 2D лучшая гиперплоскость — это просто линия

Но что такое лучшая гиперплоскость ? Для SVM это тот, который максимизирует поля от обоих тегов. Другими словами: гиперплоскость (помните, что в данном случае это линия), чье расстояние до ближайшего элемента каждого тега является наибольшим.

Не все гиперплоскости созданы равными

Вы можете посмотреть этот видеоурок, чтобы узнать, как именно находится эта оптимальная гиперплоскость.

Нелинейные данные

Теперь этот пример был простым, поскольку ясно, что данные линейно разделимы — мы могли провести прямую линию, чтобы разделить красных и синих . К сожалению, обычно все не так просто. Взгляните на этот случай:

Более сложный набор данных

Совершенно очевидно, что здесь нет линейной границы решения (одна прямая линия, разделяющая оба тега). Однако векторы очень четко разделены, и кажется, что их должно быть легко разделить.

Вот что мы сделаем: мы добавим третье измерение. До сих пор у нас было два измерения: x и y . Создаем новый размер z и правим, чтобы он вычислялся определенным удобным для нас способом: z = x² + y² (заметьте, это уравнение для окружности).

Это даст нам трехмерное пространство. Срез этого пространства выглядит так:

С другой точки зрения, данные теперь разделены на две линейно разделенные группы

Что может сделать с этим SVM? Посмотрим:

Отлично! Обратите внимание, что поскольку мы сейчас находимся в трех измерениях, гиперплоскость представляет собой плоскость, параллельную оси x на определенном расстоянии z (скажем, z = 1 ).

Осталось отобразить его обратно в два измерения:

Вернуться к нашему исходному виду, теперь все аккуратно разделено

И вот мы идем! Наша граница решения — это окружность радиусом 1, которая разделяет обе метки с помощью SVM. Посмотрите эту 3D-визуализацию, чтобы увидеть еще один пример того же эффекта:

Хитрость ядра

В нашем примере мы нашли способ классифицировать нелинейные данные, умело отображая наше пространство в более высокое измерение. Однако оказывается, что вычисление этого преобразования может стать довольно затратным с точки зрения вычислений: может быть много новых измерений, каждое из которых, возможно, требует сложных вычислений. Выполнение этого для каждого вектора в наборе данных может потребовать много работы, поэтому было бы здорово, если бы мы могли найти более дешевое решение.

И нам повезло! Вот хитрость: SVM не нужны настоящие векторы, чтобы творить чудеса, на самом деле он может обойтись только скалярными произведениями между ними. Это означает, что мы можем избежать дорогостоящих расчетов новых измерений.

Это то, что мы делаем вместо этого:

• Представьте себе новое пространство, которое мы хотим:

  z = x² + y²

• . Посмотрите на то, как выглядит точечный продукт в этом пространстве:

  a · b = xa · xb  + ya · yb  + za · zb

  a · b = xa · xb  + ya · yb +  (xa² + ya²) · (xb² + yb²)

  3

  3

  Прикажите SVM сделать свое дело, но с использованием нового скалярного произведения — мы называем это функция ядра .

Вот и все! Это трюк ядра , который позволяет нам обойти множество дорогостоящих вычислений. Обычно ядро ​​линейно, и мы получаем линейный классификатор. Однако, используя нелинейное ядро ​​(как указано выше), мы можем получить нелинейный классификатор, вообще не преобразовывая данные: мы только меняем скалярное произведение на нужное нам пространство, и SVM будет счастливо пыхтеть.

Обратите внимание, что трюк с ядром на самом деле не является частью SVM. Его можно использовать с другими линейными классификаторами, такими как логистическая регрессия. Машина опорных векторов занимается только поиском границы решения.

Использование SVM с классификацией естественного языка

Итак, мы можем классифицировать векторы в многомерном пространстве. Большой! Теперь мы хотим применить этот алгоритм для классификации текста, и первое, что нам нужно, — это способ преобразовать фрагмент текста в вектор чисел, чтобы мы могли запускать с ними SVM. Другими словами, какие функций мы должны использовать, чтобы классифицировать тексты с помощью SVM?

Самый распространенный ответ — частоты слов, как мы это делали в Наивном Байесе. Это означает, что мы относимся к тексту как к набору слов, и для каждого слова, появляющегося в этом наборе, у нас есть характеристика. Значение этой функции будет зависеть от того, насколько часто это слово встречается в тексте.

Этот метод сводится к тому, чтобы просто подсчитать, сколько раз каждое слово встречается в тексте, и разделить его на общее количество слов. Так, в предложении «Все обезьяны — приматы, но не все приматы — обезьяны» слово обезьян имеет частоту 2/10 = 0,2, а слово , но имеет частоту 1/10 = 0,1.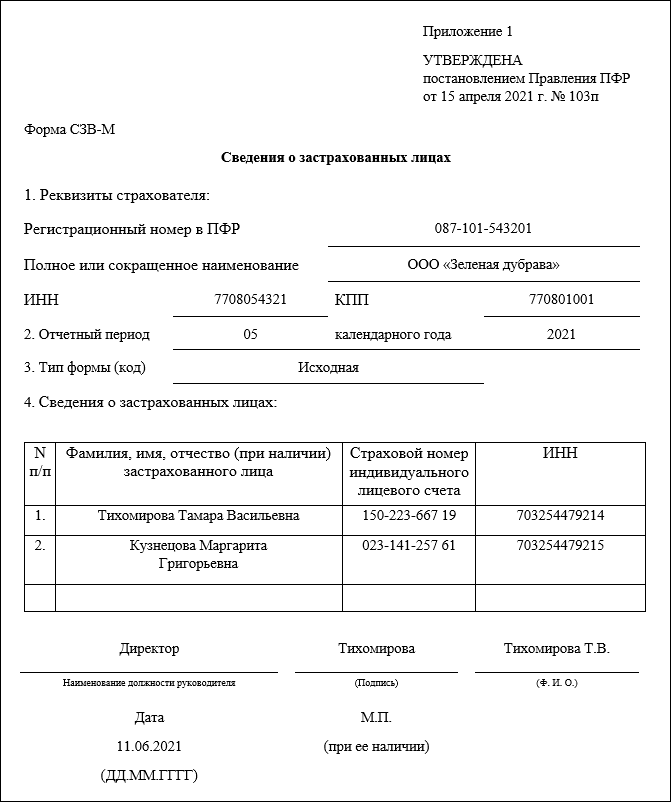

Для более продвинутой альтернативы расчета частот мы также можем использовать TF-IDF.

Теперь, когда мы это сделали, каждый текст в нашем наборе данных представлен в виде вектора с тысячами (или десятками тысяч) измерений, каждое из которых представляет частоту одного из слов текста. Идеальный! Это то, что мы скармливаем SVM для обучения. Мы можем улучшить это, используя методы предварительной обработки, такие как выделение корней, удаление стоп-слов и использование n-грамм.

Выбор функции ядра

Теперь, когда у нас есть векторы признаков, осталось только выбрать функцию ядра для нашей модели. Каждая проблема уникальна, и работа ядра зависит от того, как выглядят данные. В нашем примере наши данные были расположены концентрическими кругами, поэтому мы выбрали ядро, которое соответствовало этим точкам данных.

Принимая это во внимание, что лучше всего подходит для обработки естественного языка? Нужен ли нам нелинейный классификатор? Или данные линейно разделимы? Оказывается, лучше всего придерживаться линейного ядра. Почему?

В нашем примере у нас было две функции. Некоторые реальные применения SVM в других областях могут использовать десятки или даже сотни функций. Между тем, классификаторы НЛП используют тысяч признаков, поскольку они могут иметь до одного на каждое слово, которое появляется в обучающих данных. Это немного меняет проблему: хотя использование нелинейных ядер может быть хорошей идеей в других случаях, наличие такого количества функций в конечном итоге приведет к тому, что нелинейные ядра перекроют данные. Поэтому лучше просто придерживаться старого доброго линейного ядра, которое на самом деле дает наилучшую производительность в этих случаях.

Собираем все вместе

Осталось только потренироваться! Мы должны взять наш набор помеченных текстов, преобразовать их в векторы, используя частоты слов, и передать их алгоритму, который будет использовать выбранную нами функцию ядра, чтобы он создал модель. Затем, когда у нас есть новый неразмеченный текст, который мы хотим классифицировать, мы конвертируем его в вектор и передаем модели, которая выведет тег текста.

Учебное пособие по простому классификатору SVM

Чтобы создать собственный классификатор SVM, не заморачиваясь с векторами, ядрами и TF-IDF, вы можете сразу же приступить к работе с одной из предварительно созданных моделей классификации MonkeyLearn. Кроме того, легко создавать свои собственные благодаря интуитивно понятному пользовательскому интерфейсу платформы и подходу без кода.

Это также отлично подходит для тех, кто не хочет вкладывать большие суммы капитала в найм экспертов по машинному обучению.

Давайте покажем вам, как легко создать классификатор SVM за 8 простых шагов. Прежде чем начать, вам необходимо бесплатно зарегистрироваться в MonkeyLearn.

1. Создайте новый классификатор

Перейдите на панель инструментов, нажмите «Создать модель» и выберите «Классификатор».

2. Выберите, как вы хотите классифицировать данные

Мы собираемся выбрать модель «Тематическая классификация» для классификации текста на основе темы, аспекта или релевантности.

3. Импорт данных обучения

Выберите и загрузите данные, которые вы будете использовать для обучения модели. Имейте в виду, что классификаторы учатся и становятся умнее, когда вы предоставляете им больше обучающих данных. Вы можете импортировать данные из файлов CSV или Excel.

4. Определите теги для вашего классификатора SVM

Пришло время определить ваши теги, которые вы будете использовать для обучения вашего классификатора тем. Добавьте как минимум два тега для начала — вы всегда можете добавить больше тегов позже.

5. Отметьте данные для обучения вашего классификатора

Начните обучение вашего классификатора тем, выбрав теги для каждого примера:

После ручной пометки некоторых примеров классификатор начнет делать прогнозы самостоятельно. Если вы хотите, чтобы ваша модель была более точной, вам придется пометить больше примеров, чтобы продолжить обучение модели.

Чем больше данных вы пометите, тем умнее будет ваша модель.

6. Установите алгоритм SVM

Перейдите в настройки и убедитесь, что вы выбрали алгоритм SVM в расширенном разделе.

7. Протестируйте свой классификатор

Теперь вы можете протестировать свой классификатор SVM, нажав «Выполнить» > «Демо». Напишите свой собственный текст и посмотрите, как ваша модель классифицирует новые данные:

8. Интегрируйте классификатор тем

Вы научили свою модель делать точные прогнозы при классификации текста. Теперь пришло время загрузить новые данные! В MonkeyLearn это можно сделать тремя различными способами:

1. Пакетная обработка: перейдите в «Выполнить» > «Пакетная обработка» и загрузите файл CSV или Excel. Классификатор проанализирует ваши данные и отправит вам новый файл с прогнозами.

2. API: используйте MonkeyLearn API для классификации новых данных из любого места.

3. Интеграции: подключайте повседневные приложения для автоматического импорта новых текстовых данных в ваш классификатор. Такие интеграции, как Google Sheets, Zapier и Zendesk, можно использовать, не вводя ни одной строки кода:

Заключительные слова

И это основы работы с методами опорных векторов!

Подводя итог:

• Метод опорных векторов позволяет классифицировать данные, которые являются линейно разделимыми.
• Если это не линейно разделимо, вы можете использовать трюк с ядром, чтобы заставить его работать.
• Однако для текстовой классификации лучше придерживаться линейного ядра.

С помощью инструментов MLaaS, таких как MonkeyLearn, очень просто внедрить SVM для классификации текста и сразу же получить ценную информацию.

Есть вопросы? Запланируйте демонстрацию, и мы поможем вам начать работу.

Практическое руководство по интерпретации и визуализации машин опорных векторов | по HD

SVM часто называют «черными ящиками». В этой статье мы рассмотрим методы визуализации изученных моделей SVM и их производительности на реальных данных.

Изображение Снято Хьюго Доланом

Об авторе

Хьюго Долан изучает финансовую математику в Университетском колледже Дублина. Это в основном основано и мотивировано недавним опытом анализа данных и машинного обучения в конкурсе NFL Punt Analytics Kaggle, а также участием в команде, выигравшей Citadel Dublin Data Open, а также материалами из Стэнфордского университета CS229.онлайн курс.

Эта статья содержит следующие разделы:

1. Введение в линейные модели, SVM и ядра
2. Интерпретация многомерных инженерных пространств признаков, использующих ядра SVM…
3. Методы оценки производительности высокоразмерных границ
4. Практические варианты работы с большими дисбалансами классов
5. Сколько данных нужно для обучения SVM

Некоторые предположения, которые я сделаю:

В этой статье предполагается знакомство с основными моделями машинного обучения, такими как логистическая и линейная регрессия. Это также предполагает, что вы знаете, как рисовать некоторые графики, которые я обсуждаю (у меня есть руководство для этого, если вы застряли!). Мы также предполагаем, что вы знаете, что такое функция решения и функция цели / стоимости, и что у вас есть базовые знания линейной алгебры. Если это все еще не стоит прочтения, вы всегда можете добавить это в закладки и вернуться позже для более глубокого изучения некоторых математических частей этой статьи.

Введение в линейные модели, SVM и ядра

В машинном обучении линейные классификаторы — это любые модели, в которых существует единственная функция гипотезы, которая отображает входные данные модели и прогнозируемые выходные данные.

Многие модели, такие как логистическая регрессия, наивный байесовский анализ и дискриминантный анализ, являются примерами линейных моделей.

Основным преимуществом линейных моделей перед нейронными сетями (нелинейными моделями) является то, что веса признаков напрямую соответствуют важности признака в модели. Таким образом, легко понять, чему модель «научилась».

При обучении модели регуляризованной регрессии L1 сразу становится очевидным, что большинство наших функций в нашем наборе данных совершенно не имеют отношения к прогнозированию нашего результата. Ясно, что признаки 0,1 вносят положительный вклад в модель, в то время как наличие признаков 2,3,4 в данном примере приводит к отрицательному вкладу в результат

. В основе любой линейной модели лежит скалярное произведение между входной пример и вектор параметра/веса. В случае линейной регрессии это вся функция гипотезы. В то время как логистическая регрессия передает точечный продукт через сигмовидную функцию, так что результат находится в диапазоне от 0 до 1 и, следовательно, подходит для задач двоичной классификации.

При рассмотрении задач классификации падение линейных моделей заключается в том, что в конечном итоге граница решения представляет собой прямую линию, плоскость или гиперплоскость с коэффициентами, равными весам/параметрам моделей, и, таким образом, могут классифицировать только данные, которые являются линейно разделимыми, что может быть большим ограничение при работе над более сложными задачами аналитики.

Как мы видим, простая линейная модель не может разделить две «шумные гиперболы», так как она может соответствовать только «прямой» плоскости/линии через данные. Во втором примере используется нелинейная модель (на самом деле это трюк ядра, мы скоро к этому вернемся)

Машина опорных векторов (SVM) — единственная линейная модель, которая может классифицировать данные, которые не являются линейно разделимыми.

Вы можете спросить, как SVM, являющийся линейной моделью, может подогнать линейный классификатор к нелинейным данным. Интуитивно с помощью простой модели линейной регрессии мы можем вручную спроектировать функции x, x², x³,…, чтобы попытаться добиться соответствия нелинейному набору точек данных.

Хотя характеристика X является единственной независимой переменной, которую мы должны предсказать для y, которая по своей природе имеет нелинейную связь с x, мы можем спроектировать характеристики x² и x³, чтобы улучшить нашу подгонку к y.

Перенося эту интуицию в нашу SVM, когда мы разрабатываем функцию x², мы, по сути, умножаем функцию x саму на себя. Итак, предположим, что мы проектируем функции из нашего набора данных, перемножая комбинации функций x1,x2,x3… вместе, тогда теоретически мы *могли бы* получить пространство, в котором ваши инженерные функции линейно разделимы. Взяв предыдущий простой пример, посмотрите, как приведенные ниже данные преобразуются в почти линейный тренд в пространстве признаков x³.

В качестве дополнительной интуиции по отношению к предыдущему примеру мы можем увидеть, преобразовав ось x из исходного пространства признаков x в пространство признаков x³, как модель можно рассматривать как линейную зависимость между x³ и y.

К сожалению, для достижения этого со сложным набором данных требуется создать больше, чем просто трехмерное пространство (признаки x, x²,x³), но на самом деле пространства признаков чрезвычайно высокой размерности, вычисление которых для каждого примера в нашем наборе данных было бы очень затратным в вычислительном отношении. Ниже я покажу пример функции ø(x), которая берет наши исходные функции x и объединяет их для создания множества полиномиальных функций 2-го порядка.

Прежде чем мы продолжим : я буду использовать обозначение x для обозначения точек данных / обучающих примеров с верхними индексами для обозначения конкретной точки данных и нижними индексами для обозначения конкретной функции.

Это обычно многомерное пространство, если бы у нас было 100 функций изначально, то эта функция произвела бы 100 * 100 спроектированных функций. Это требует больших вычислительных ресурсов, в данном случае временная сложность Big-O(n²), подумайте о необходимости написать два вложенных цикла for для генерации всех комбинаций, создаваемых ø(x).

К счастью для нас, есть выход из этой загадки вычислительной сложности! Когда мы выводим задачу оптимизации для SVM (сложно выглядящая формула, которая говорит нам, как получить и обновить наши веса для максимизации во время подъема координат), оказывается, что наши векторы признаков для нашего тренировочного входа x появляются только в одном месте в пределах вся формула оптимизации (выделена красным).

Этот скалярный продукт был для нашего исходного пространства признаков, поэтому теперь давайте заменим его нашим пространством признаков инженера, используя нашу функцию ø.

Так как же это поможет снизить вычислительную сложность? По определению скалярного произведения мы берем i-й элемент ø(x(i)) и умножаем его на i-й элемент ø(x(j)) и затем суммируем все это, чтобы получить одиночный скейлер. Применяя это, мы получаем:

Как будто по волшебству мы можем полностью избавиться от необходимости вычислять ø(x) с помощью простых алгебраических манипуляций с помощью трюка с ядром. Теперь у нас есть все преимущества многомерного пространства признаков без дополнительной вычислительной сложности 9j) ):

Простая замена, обратите внимание, что наше ядро ​​использует x и z здесь только для того, чтобы удалить обозначение надстрочного индекса.

Точно так же, когда мы хотим использовать нашу модель для прогнозирования, мы никогда явно не вычисляем веса для нашего многомерного пространства, а вместо этого используем трюк ядра, чтобы сделать наши прогнозы:

Таким образом, мы можем использовать трюк ядра для преобразования нелинейного набор данных в набор данных, который является линейно разделимым, только в пространстве более высокой размерности. Sklearn поставляется с несколькими ядрами в реализации SVC, включая Radius Basis Kernel (RBF) и Polynomial Kernels, каждое из которых имеет свои собственные гиперпараметры, которые можно настроить экспериментально с помощью перекрестной проверки для достижения наилучших результатов.

Небольшая заминка, интерпретация многомерного спроектированного пространства признаков…

Итак, помните, как мы говорили, что большое преимущество линейной модели заключается в том, что веса/параметры модели можно интерпретировать как важность признаков. Что ж, это исчезает, как только мы разрабатываем многомерный или бесконечный набор признаков, веса модели неявно соответствуют многомерному пространству, что бесполезно для нашего понимания.

Вместо этого мы можем подобрать модель логистической регрессии, которая оценивает вероятность того, что метка y будет равна 1, при заданных исходных функциях, где f(x) — функция принятия решения SVM:

Если это кажется вам знакомым, подумайте о логистической регрессии!

Мы используем оценку максимального правдоподобия, чтобы соответствовать параметрам этой модели логистической регрессии, метод называется Масштабирование Платта, оригинальную статью [3], безусловно, стоит прочитать, если вам интересно узнать о внутренней работе.

Так как же это поможет нам понять, как работает SVM? Что ж, мы просто подгоняем модель и выбираем точку в нашем наборе данных для ее оценки, затем возмущаем одну функцию за раз через диапазон значений, сохраняя при этом другие функции фиксированными. Мы можем использовать это, чтобы нарисовать график чувствительности модели к каждой функции.

SKlearn поставляется с этой функцией, встроенной в модель SVC, вам просто нужно убедиться, что вероятность = true, при инициализации, а затем использовать clf. predict_proba(X) функция для получения вероятностей.

На практике я обнаружил, что вместо того, чтобы просто оценивать одну точку, часто лучше выбрать набор соответствующих точек, например. 40 отрицательных примеров и усреднить распределение вероятности по признаку, чтобы получить что-то более репрезентативное.

Вот пример, который я сделал, когда работал над соревнованием NFL Punt Analytics Kaggle, изучая влияние различных факторов на сотрясение мозга:

Я взял все отрицательные примеры и усреднил их вероятности, я выделил области красным для каждой функции, где игроки с наибольшей вероятностью могли получить сотрясение мозга. Уловка, если у вас есть куча одной горячей закодированной переменной, такой как роль игрока, состоит в том, чтобы объединить их в гистограмму и просто посмотреть на чистое изменение вероятности между тем, когда функция присутствует и не присутствует.

Также есть отличный пример применения этого к маркетинговым данным [1], который вы можете найти здесь. Я также хотел бы поблагодарить Георгия, который нашел время, чтобы ответить на некоторые из моих вопросов о статье.

Методы оценки производительности

Когда вы имеете дело с многомерными моделями, включающими SVM, было бы неплохо иметь возможность визуализировать, как модель классифицирует точки данных, не полагаясь исключительно на такие показатели, как оценки F1 или ROC AUC.

Хотя некоторые могут использовать такие методы, как анализ основных компонентов, для визуализации классификации, при этом мы теряем размеры нашего пространства признаков и, таким образом, искажаем визуальное представление, которое хотим получить.

Я нашел хороший метод, который называется «Гистограмма проектов» [2]. Он включает в себя графическое распределение выходных данных функции принятия решения SVM для ваших обучающих и тестовых наборов.

Функцию принятия решения легко получить в реализации SKlearn SVC, просто вызвав solution_function(X). Вам потребуется отслеживать метки наборов данных, чтобы можно было раскрасить гистограмму проекций, как показано ниже:

Гистограмму проекций довольно легко интерпретировать. Ось x гистограммы определяет расстояние конкретного обучающего примера от границы решения SVM (обозначенной центральной пунктирной линией).

SVM имеет границу разделения, равную 1 по обе стороны от границы решения, это принудительное ограничение задачи двойной оптимизации («Опорные векторы» — это точки данных, которые лежат вдоль этих границ). Вы заметите, что в приведенной выше модели есть некоторая утечка в области маржи и действительно переход от одного класса к классу на противоположной стороне границы решения. Это связано с тем, что мы установили гиперпараметр регуляризации C > 0 (это позволяет найти компромисс между некоторой неправильной классификацией и минимизацией целевой функции SVM).

Несмотря на работу с пространствами признаков большой размерности, эта диаграмма успешно визуализирует область границы решения и всю классификацию без потери размерности. Все показатели, отображаемые в матрице путаницы (т. е. количество истинно положительных, ложноположительных, истинно отрицательных и ложноотрицательных результатов), также можно увидеть на гистограмме. Это также позволяет нам наблюдать, хорошо ли модель обобщает тестовый набор. Если тестовый набор имеет такое же распределение выходных данных функции принятия решений, что и обучающий набор, то мы можем сказать, что модель имеет хорошие характеристики при обобщении. Модель также может использоваться для определения того, является ли набор данных линейно разделимым с учетом выбранных гиперпараметров.

Практические варианты работы с несбалансированными данными

Когда набор данных имеет непропорциональное количество примеров для одного класса по сравнению с другим, мы говорим, что он несбалансирован.

Пример реального набора данных с дисбалансом более 3000:1

Это проблема, если мы хотим построить модель ML для прогнозирования появления меньшинства, поскольку мы можем достичь высокого уровня точности, просто неправильно классифицируя все меньшинство примеры как класс большинства.

Это часто происходит в реальных данных, будь то выявление злокачественных тканей, мошенничество с кредитными картами или сотрясения мозга в спорте, из-за относительной редкости инцидентов, которые мы хотим правильно идентифицировать.

Существует два общепринятых метода исправления моделей машинного обучения, работающих с несбалансированными данными:

1. Избыточная выборка класса меньшинства / недостаточная выборка класса большинства
2. Увеличение веса для примеров меньшинства в функции стоимости 1 : SMOTE

   Существует два способа повторной выборки данных: удаление существующих примеров (недостаточная выборка) или добавление новых примеров (избыточная выборка). Наиболее общепринятым методом является избыточная выборка класса меньшинства с использованием алгоритма, называемого SMOTE (Synthetic Minority Oversampling Technique) [5] 9.0003

   Это намного проще, чем следует из названия, для каждой точки меньшинства в наборе данных он выбирает k ближайших других примеров меньшинства (обычно 5) и интерполирует случайно новые примеры меньшинств вдоль линии, «соединяющей» существующие примеры меньшинств.

   Это разумно, так как мы просто делаем предположение, что путем интерполяции между похожими существующими примерами мы получим новые примеры того же класса.

   Мы видим, как SMOTE генерирует новые точки данных вдоль линий существующих точек

   Это имеет тенденцию значительно улучшать производительность модели и помогает обобщить границу решения для примеров меньшинства.

   Вариант 2: Введение весов в целевую функцию

   Другая процедура, которую можно использовать, заключается в назначении более высоких весов в целевой функции для неправильной классификации примеров меньшинства. Это «стимулирует» алгоритм правильно классифицировать классы меньшинств.

   У меня нет личного опыта использования этого метода, но его можно использовать в сочетании с вариантом 1. Это ссылка на хорошую статью здесь [4], в которой подробно описаны многие подходы к работе с дисбалансом классов

   Сколько данных мне нужно для обучения SVM

   Разумным эмпирическим правилом является как минимум примерно в 10 раз больше обучающих примеров, чем признаков. Если у вас есть большой объем обучающих данных, лучше всего использовать менее 50 000 обучающих примеров, поскольку реализация SVC в sklearn имеет сложность O (n³), а это означает, что время сходимости к решению растет кубически с количеством обучающих примеров, оно может становятся довольно медленными даже на приличном ноутбуке или контейнере kaggle.

   Часто стоит сначала потренироваться на меньшем наборе данных и настроить гиперпараметры вашей модели. Вы можете сохранить небольшой набор тестов перекрестной проверки для выбора модели. Вы можете быть удивлены тем, насколько хорошо ваша модель обобщает, когда вы тестируете оставшийся набор данных, несмотря на небольшую долю фактических данных, которые вы, возможно, использовали.

   Примечание. Если вы новичок в этом, совет состоит в том, чтобы использовать разделительный модуль для обучения поездов sklearn и исправить случайное начальное число, чтобы ваши результаты были воспроизводимыми, если вам случится вернуться, чтобы отредактировать какой-либо более ранний код и повторно запустить обучение / Процедура выбора модели.

   Я надеюсь, что эта статья была полезной, если у вас есть какие-либо комментарии / вопросы, оставьте их ниже, я постараюсь ответить на них, насколько смогу.

   Ссылки на документы

   [1] Налбантов, Георги и К. Биох, Ян и Гроенен, Патрик. (2005). Решение и интерпретация задач бинарной классификации в маркетинге с помощью SVM. 566–573. 10.1007/3–540–31314–1_69.

   [2] Черкасский, Владимир и Дхар, Сауптик. (2010).