Среднее квадратичное отклонение онлайн калькулятор 44 фз: Среднее квадратичное отклонение | Онлайн калькулятор

Калькулятор Среднеквадратичное Отклонение

Онлайн-калькулятор среднеквадратичное отклонение поможет вам среднеквадратичное отклонение калькулятор, дисперсию, среднее значение и сумму квадратов набора данных. Низкое значение стандартного отклонения указывает на то, что точки близки к среднему значению, тогда как большее значение указывает на то, что числа сильно отличаются от среднего. Среднее также известно как среднее значение чисел в наборе данных. Наш калькулятор среднего и SD работает для следующих двух наборов данных:

• Для образца
• Для населения

Стандартное отклонение – это одна из мер дисперсии, которая говорит нам, насколько значения в наборе данных отличаются от среднего. Это квадратный корень из дисперсии набора данных. Кроме того, он часто используется для измерения статистических результатов, например, погрешности. В этом случае стандартное отклонение называется стандартной ошибкой среднего. Для удобства вы можете попробовать наш онлайн-калькулятор среднеквадратическое отклонение ошибки, который поможет вам рассчитать стандартную ошибку для данного набора исходных данных. n \)

Кроме того, этот простой, но высокоточный калькулятор ковариации будет эффективно оценивать ковариацию между двумя случайными величинами X и Y во время экспериментов по вероятности и статистике.

Применение стандартного отклонения:

Стандартное отклонение широко используется для тестирования моделей на реальных данных экспериментально и в промышленных условиях. Его можно использовать, чтобы найти минимальную и максимальную стоимость некоторого продукта, когда продукт имеет высокий процент. Если значения выходят за пределы допустимого диапазона, то необходимо изменить производство, чтобы улучшить качество продукта. Этот показатель дисперсии широко используется в различных областях науки, например, в прогнозировании погоды для прогнозирования погоды, в финансах для измерения колебаний цен на продукцию и многих других. Вы можете легко определить нормальный или средний диапазон набора данных чего угодно с помощью решателя стандартных отклонений. Это широко используется в области социальных наук в исследовательских целях для анализа статистики здоровья, результатов тестов и демонстрации различных моделей культурного поведения.

Как найти стандартное отклонение (шаг за шагом):

Наш среднего и калькулятор среднеквадратическое отклонение выполняет мгновенные вычисления, чтобы найти статистическую меру разнообразия или изменчивости в наборе данных, который является S.D. Вам просто нужно следовать следующим пунктам, чтобы производить точные вычисления вручную:

• Узнайте количество выборки из совокупности
• Рассчитать среднее
• Найдите разницу между каждым образцом и средним значением
• Возвести каждое значение в квадрат
• Найдите сумму квадратов каждого значения
• Разделите на N-1, чтобы получить дисперсию набора данных.
• Взяв квадратный корень из значения, вы можете определить калькулятор среднее квадратическое отклонение набора данных.

Здесь у нас есть пример решения вручную для лучшего понимания.

Читать дальше!

Пример:
Найти стандартное отклонение от среднего для выборки с 6 числами 3, 4, 9, 7, 2, 5?

Решение:

Шаг 1:

Вычислите среднее значение чисел, для этого разделите сумму всех чисел на общее число:

\ (µ = {\ frac {3 + 4 + 9 + 7 + 2 + 5} {6}} \)

\ (µ = 30/6 \)

\ (µ = 5 \)

Шаг 2:

Найдите квадрат разницы каждого значения со средним значением:

\ (x_1-µ = 3 – 5 = -2 \)

\ (x_2-µ = 4 – 5 = -1 \)

\ (x_3-µ = 9 – 5 = 4 \)

\ (x_4-µ = 7 – 5 = 2 \)

\ (x_5-µ = 2 – 5 = -3 \)

\ (x_6-µ = 5 – 5 = 0 \)

Сейчас же,

\ ((x_1-µ) ^ 2 = (-2) ^ 2 = 4 \)

\ ((x_2-µ) ^ 2 = (-1) ^ 2 = 1 \)

\ ((x_3-µ) ^ 2 = (-4) ^ 2 = 16 \)

\ ((x_4-µ) ^ 2 = (2) ^ 2 = 4 \)

\ ((x_5-µ) ^ 2 = (-3) ^ 2 = 9 \)

\ ((x_6-µ) ^ 2 = (0) ^ 2 = 0 \)

Шаг 3:

Вычислить стандартное отклонение:

\ (s = \ sqrt {\ frac {4 + 1 + 16 + 4 + 9 + 0} {6-1}} \)

\ (s = \ sqrt {\ frac {34} {5}} \)

\ (s = \ sqrt {6. 2 = 6,8 \)

Просто учтите этот калькулятор среднеквадратичное отклонение и введите значения в соответствующие поля. Калькулятор дисперсии и стандартного отклонения помогает выполнять вычисления как для простых, так и для сложных вычислений стандартных отклонений и дисперсии.

Стандартное отклонение в гистограммах:

Набор данных представлен в виде гистограммы, которая представляет числа в виде полос разной высоты. На гистограмме столбцы представляют диапазон набора данных. Более длинный столбец представляет более высокий диапазон набора данных, в то время как более широкий столбец указывает на большее стандартное отклонение, а более узкий столбец указывает на меньшее стандартное отклонение. Приведем пример:

Тестовые отметки 600 студентов со средним значением 100, ориентация гистограммы следующая:

Оценки за тесты по математике SD = 8,5

Оценки по английскому языку SD = 18,3

Оценки по физике SD = 25,8

По всем трем предметам тест по физике имеет самое высокое стандартное отклонение.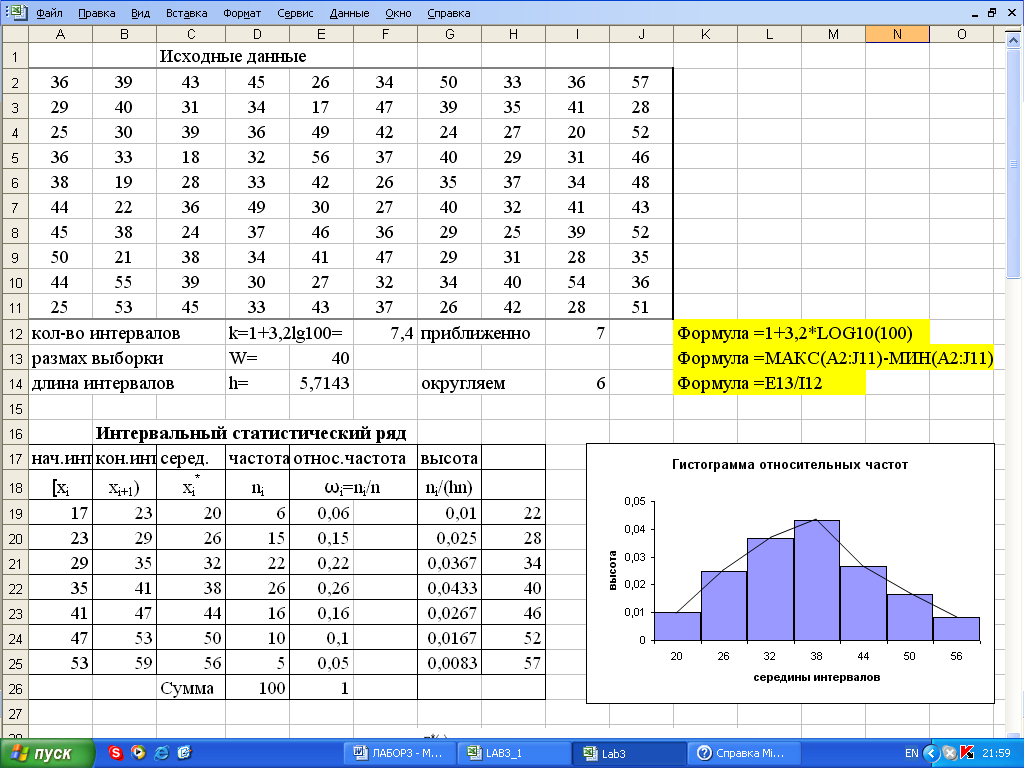

Как среднеквадратичное отклонение калькулятор с помощью калькулятора SD:

Несомненно, вычисление стандартного отклонения набора данных – непростая задача. Но наш калькулятор SD лучше всего подходит для быстрого определения S.D.

Входы:

• Сначала выберите вариант: значение вашего набора данных в форме выборки или генеральной совокупности.
• Затем введите значения для набора данных
• Наконец, нажмите кнопку расчета

Выходы:

Калькулятор показывает:

• Стандартное отклонение набора данных
• Дисперсия набора данных
• Среднее значение набора данных
• Всего чисел
• Сумма квадратов чисел
• Пошаговый расчет

Этот поисковик stdev использует ваш набор данных и отображает всю работу, необходимую для ваших расчетов.

Конечное примечание:

Стандартное отклонение называется мерой разброса чисел в данном наборе данных от его среднего значения. Эта статистическая модель используется почти во всех областях, включая исследования финансового рынка, прогноз климата, фармацевтику, материаловедение и т. Д. калькулятор среднее квадратическое отклонение помогает исследователю проводить эксперименты, когда сбор всех данных невозможен. Когда дело доходит до расчета стандартного отклонения, это очень сложно сделать вручную. Поэтому для удобства попробуйте этот онлайн-калькулятор среднеквадратичное отклонение , который поможет вам определить стандартное отклонение набора данных с другими статистическими показателями.

Other Languages: Standard Deviation Calculator, Standart Sapma Hesaplama, Odchylenie Standardowe Kalkulator, Kalkulator Standar Deviasi, Standardabweichung Rechner, 標準偏差 計算, 표준편차 계산기, výpočet směrodatné odchylky, Calculadora De Desvio Padrão, Calculadora De Desviacion Estandar, Calcul Ecart Type, Calcolo Deviazione Standard Online, حساب الانحراف المعياري, Keskihajonta Laskin.

Оптимальный алгоритм игры в морской бой / Хабр

Пару дней назад я с удивлением узнал, что некоторые мои знакомые не умеют играть в морской бой. Т.е. правила они, конечно, знают, но вот играют как-то бессистемно и в итоге часто проигрывают. В этой записи я постараюсь изложить основные идеи, которые помогут повысить уровень вашей игры.

Правила игры

Существует множество вариантов морского боя, но мы с вами рассмотрим наиболее распространённый вариант со следующим набором кораблей:

Все перечисленные корабли должны быть размещены на квадратном поле 10 на 10 клеток, при этом корабли не могут соприкасаться ни углами, ни сторонами. Самое игровое поле нумеруется сверху вниз, а вертикали помечаются русскими буквами от «А» до «К» (при этом буквы «Ё» и «Й» пропускают).

Рядом рисуется вражеское поле аналогичного размера. При удачном выстреле по кораблю противника на соответствующей клетке вражеского поля ставится крестик и производится повторный выстрел, при неудачном выстреле в соответствующей клетке ставится точка, и ход переходит к противнику.

Оптимальная стратегия

В игре морской бой всегда есть элемент случайности, но его можно свести к минимуму. Прежде чем переходить непосредственно к поиску оптимальной стратегии, необходимо озвучить одну очевидную вещь: вероятность попасть по кораблю противника тем выше, чем меньше непроверенных клеток осталось на его поле, аналогично вероятность попадания по вашим кораблям тем ниже, чем больше непровереных клеток осталось на вашем поле. Т.о. для эффективной игры нужно научиться сразу двум вещам: оптимальной стрельбе по противнику и оптимальному своих размещению кораблей.

В дальнейшем объяснении будут использоваться следующие обозначения:

Оптимальная стрельба

Первым и самым очевидным правилом оптимальной стрельбы является следующее правило: не стрелять по клеткам непосредственно окружающим уничтоженный корабль противника.

В соответствии с принятыми выше обозначениями, на рисунке жёлтым отмечены те клетки, по которым уже были произведены безуспешные выстрелы, красным отмечены клетки, выстрелы по которым закончились попаданием, а зелёным отмечены клетки, стрельба по которым не производилась, но можно гарантировано утверждать, что кораблей в них нет (кораблей там быть не может, т. к. по правилам игры корабли не могут соприкасаться).

Из первого правила сразу вытекает второе: если вам удалось подбить вражеский корабль, необходимо сразу же его добить, чтобы как можно раньше получить список гарантировано свободных клеток.

Третье правило вытекает из первых двух: необходимо в первую очередь пытаться подбить самые крупные корабли противника. Возможно, для вас это правило не очевидно, но если немного подумать, то можно легко заметить, что уничтожив вражеский линкор, мы в лучшем случае получим информацию сразу о 14 гарантировано свободных клетках, а уничтожив крейсер, всего о 12.

Т.о. оптимальную стратегию стрельбы можно свести к целенаправленному поиску и уничтожению самых крупных кораблей противника. К сожалению, сформулировать стратегию мало, необходимо предложить способ её реализации.

Для начала давайте рассмотрим участок игрового поля размером 4 на 4 клетки. Если в рассматриваемом участке есть вражеский линкор, то его гарантировано можно подбить не более чем за 4 выстрела. Для этого надо стрелять так, чтобы на каждой горизонтали и вертикали было ровно по одной проверенной клетке. ниже представлены все варианты такой стрельбы (без учёта отражений и поворотов).

Среди всех этих вариантов, оптимальными на поле 10 на 10 клеток являются только первые два варианта, гарантирующие попадание в линкор максимум за 24 выстрела.

После того, как уничтожен вражеский линкор, необходимо начинать поиск крейсеров, а затем и эсминцев. При этом, как вы уже догадались, можно воспользоваться аналогичной методикой. Только теперь необходимо разбивать поле на квадраты со стороной в 3 и 2 клетки соответственно.

Если при поиске линкора вы использовали вторую стратегию, то для поиска крейсеров и эсминцев вам необходимо стрелять по следующим полям (зелёным отмечены поля, по которым вы уже стреляли при поиске линкора):

Для поиска катеров оптимальной стратегии не существует, поэтому в конце игры приходится опираться в основном на удачу.

Оптимальное размещение кораблей

Оптимальная стратегия размещения кораблей в некотором смысле обратна оптимальной стратегии стрельбы. При стрельбе, мы пытались найти самые крупные корабли, чтобы сократить количество клеток, которые нужно проверять, за счёт гарантировано свободных клеток. Значит, при размещении корабли надо ставить таким образом, чтобы в случае их потери минимизировать количество гарантировано свободных клеток. Как вы помните, линкор в центре поля открывает для противника сразу 14 полей, но линкор, стоящий в углу, открывает для противника всего 6 полей:

Аналогично, крейсер, стоящий в углу, вместо 12 полей открывает всего 6. Т.о., разместив крупные корабли вдоль границы поля, вы оставляете больший простор для катеров. Т.к. стратегии для поиска катеров нет, противнику придётся стрелять наугад, и чем больше свободных полей у вас останется к моменту ловли катеров, тем тяжелее будет выиграть противнику.

Ниже представлено три способа размещения крупных кораблей, которые оставляют большой простор для катеров (отмечено синим):

Каждая из приведённых расстановок оставляет для катеров ровно 60 свободных клеток, а это значит, что вероятность случайно попасть в катер составляет 0,066. Для сравнения стоит привести случайную расстановку кораблей:

При такой расстановке для катеров остаётся всего 21 клетка, а это значит, что вероятность попадания по катеру составляет уже 0,19, т.е. почти в 3 раза выше.

В заключение хочу сказать, что не стоит проводить уж слишком много времени, играя в морской бой. Особенно хочу предостеречь вас от игры на лекциях. Когда я сидел в Ваби-Саби и играл в морской бой со своей девушкой, мимо прошла официантка и сказала, что она весьма неплохо играет, т.к. много практиковалась на парах. Кто знает, кем бы она работала, если бы в своё время слушала лекции?

P.S. В комментариях абсолютно верно указывают, что на хабре уже были похожие публикации, было бы неверно не поставить ссылки на них:

habrahabr.ru/post/82221

Калькулятор стандартного отклонения

Укажите числа, разделенные запятыми, для расчета стандартного отклонения, дисперсии, среднего значения, суммы и погрешности.

Калькулятор связанных вероятностей | Калькулятор размера выборки | Калькулятор статистики

Стандартное отклонение в статистике, обычно обозначаемое как σ , является мерой вариации или дисперсии (относится к степени растяжения или сжатия распределения) между значениями в наборе данных. Чем ниже стандартное отклонение, тем ближе точки данных к среднему (или ожидаемому значению)9.0006 мк . И наоборот, более высокое стандартное отклонение указывает на более широкий диапазон значений. Подобно другим математическим и статистическим понятиям, существует множество различных ситуаций, в которых можно использовать стандартное отклонение, и, следовательно, множество различных уравнений. В дополнение к выражению изменчивости населения стандартное отклонение также часто используется для измерения статистических результатов, таких как предел погрешности. При таком использовании стандартное отклонение часто называют стандартной ошибкой среднего или стандартной ошибкой оценки относительно среднего. Приведенный выше калькулятор вычисляет стандартное отклонение генеральной совокупности и стандартное отклонение выборки, а также приближения доверительного интервала.

Стандартное отклонение совокупности

Стандартное отклонение совокупности, стандартное определение σ , используется, когда можно измерить всю совокупность, и представляет собой квадратный корень из дисперсии заданного набора данных. В случаях, когда каждый член совокупности может быть отобран, для определения стандартного отклонения всей совокупности можно использовать следующее уравнение:

Для тех, кто не знаком с обозначениями суммирования, приведенное выше уравнение может показаться сложным, но если рассматривать его отдельные компоненты, это суммирование не представляет особой сложности. i=1 в суммировании указывает начальный индекс, т. е. для набора данных 1, 3, 4, 7, 8, i=1 будет 1, i=2 будет 3 и т. д. . Следовательно, обозначение суммирования просто означает выполнение операции (x _i — μ) ² для каждого значения до N , что в данном случае равно 5, поскольку в этом наборе данных 5 значений.

ПРИМЕР:           μ = (1+3+4+7+8) / 5 = 4,6        
σ = √[(1 — 4,6) ² + (3 — 4,6) ² + . .. + (8 — 4,6) ² )]/5
σ = √(12,96 + 2,56 + 0,36 + 5,76 + 11,56)/5 = 2,577

Стандартное отклонение выборки

Во многих случаях невозможно провести выборку каждого члена совокупности, что требует изменения приведенного выше уравнения таким образом, чтобы стандартное отклонение можно было измерить с помощью случайной выборки изучаемой совокупности. Общая оценка для σ — стандартное отклонение выборки, обычно обозначаемое как s . Стоит отметить, что существует множество различных уравнений для расчета стандартного отклонения выборки, поскольку, в отличие от среднего значения выборки, стандартное отклонение выборки не имеет какой-либо единственной оценки, которая была бы беспристрастной, эффективной и имела максимальную вероятность. Уравнение, представленное ниже, представляет собой «скорректированное стандартное отклонение выборки». Это скорректированная версия уравнения, полученная путем изменения уравнения стандартного отклонения совокупности с использованием размера выборки в качестве размера совокупности, что устраняет некоторую погрешность в уравнении. Однако беспристрастная оценка стандартного отклонения очень сложна и варьируется в зависимости от распределения. Таким образом, «скорректированное стандартное отклонение выборки» является наиболее часто используемой оценкой стандартного отклонения генеральной совокупности и обычно называется просто «стандартным отклонением выборки». Это гораздо лучшая оценка, чем ее нескорректированная версия, но все же она имеет значительную погрешность для малых размеров выборки (N

Пример работы с суммированием см. в разделе «Стандартное отклонение генеральной совокупности». Уравнение по существу такое же, за исключением члена N-1 в уравнении скорректированного выборочного отклонения и использования выборочных значений.

Применение стандартного отклонения

Стандартное отклонение широко используется в экспериментальных и промышленных условиях для проверки моделей на реальных данных. Примером этого в промышленных приложениях является контроль качества некоторых продуктов. Стандартное отклонение можно использовать для расчета минимального и максимального значения, в пределах которого должен находиться какой-либо аспект продукта в течение некоторого большого процента времени. В случаях, когда значения выходят за расчетный диапазон, может потребоваться внести изменения в производственный процесс для обеспечения контроля качества.

Стандартное отклонение также используется в погоде для определения различий в региональном климате. Представьте себе два города, один на побережье и один в глубине страны, в которых средняя температура одинакова — 75°F. Хотя это может привести к убеждению, что температуры в этих двух городах практически одинаковы, реальность может быть замаскирована, если учитывать только среднее значение и игнорировать стандартное отклонение. Прибрежные города, как правило, имеют гораздо более стабильную температуру из-за регулирования большими водоемами, поскольку вода имеет более высокую теплоемкость, чем земля; по сути, это делает воду гораздо менее восприимчивой к изменениям температуры, а прибрежные районы остаются теплее зимой и прохладнее летом из-за количества энергии, необходимой для изменения температуры воды. Следовательно, в то время как прибрежный город может иметь диапазон температур от 60 ° F до 85 ° F в течение определенного периода времени, что приводит к среднему значению 75 ° F, внутренний город может иметь температуру от 30 ° F до 110 ° F. получается одно и то же среднее.

Еще одной областью, в которой широко используется стандартное отклонение, являются финансы, где оно часто используется для измерения риска, связанного с колебаниями цен на некоторые активы или портфели активов. Использование стандартного отклонения в этих случаях обеспечивает оценку неопределенности будущих доходов от данной инвестиции. Например, при сравнении акции А со средней доходностью 7 % и стандартным отклонением 10 % с акцией Б, имеющей такую ​​же среднюю доходность, но со стандартным отклонением 50 %, первая акция явно будет более безопасным вариантом. поскольку стандартное отклонение акции B значительно больше при той же доходности. Это не означает, что акции А определенно являются лучшим вариантом для инвестиций в этом сценарии, поскольку стандартное отклонение может искажать среднее значение в любом направлении. В то время как Акция А имеет более высокую вероятность средней доходности, близкой к 7%, Акция Б потенциально может обеспечить значительно большую прибыль (или убыток).

Это лишь несколько примеров того, как можно использовать стандартное отклонение, но существует гораздо больше. Как правило, вычисление стандартного отклонения полезно всякий раз, когда требуется узнать, насколько далеко от среднего может быть типичное значение распределения.

Калькулятор стандартного отклонения

Использование калькулятора

Стандартное отклонение — это статистическая мера разнообразия или изменчивости в наборе данных. Низкое стандартное отклонение указывает на то, что точки данных обычно близки к среднему или среднему значению. Высокое стандартное отклонение указывает на большую изменчивость точек данных или более высокий разброс от среднего значения.

Этот калькулятор стандартного отклонения использует ваш набор данных и показывает работу, необходимую для расчетов.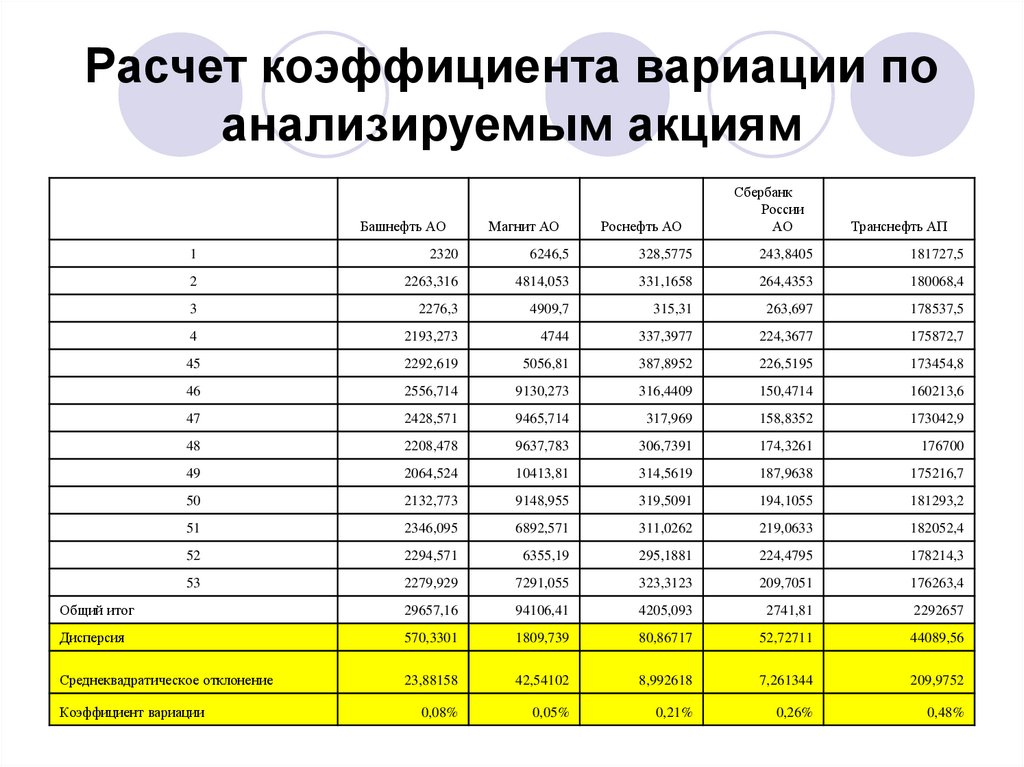

Введите набор данных, разделенный пробелами, запятыми или разрывами строк. Нажмите «Рассчитать», чтобы найти стандартное отклонение, дисперсию, количество точек данных.
n , среднее значение и сумма квадратов. Вы также можете увидеть работу, выполненную для расчета.

Вы можете копировать и вставлять строки точек данных из таких документов, как электронные таблицы Excel или текстовые документы, с запятыми или без них в форматах, показанных в таблице ниже.

Формула стандартного отклонения

Стандартное отклонение набора данных представляет собой квадратный корень из рассчитанной дисперсии набора данных.

Формула дисперсии (s ² ) представляет собой сумму квадратов разностей между каждой точкой данных и средним значением, деленную на количество точек данных.

При работе с данными из полной совокупности сумма квадратов разностей между каждой точкой данных и средним значением делится на размер набора данных,
92} \)

Для дополнительного объяснения стандартного отклонения и того, как оно связано с распределением кривой нормального распределения, см.